RIVM over Corona strategie aan de Tweede Kamer: Een bedroevende vertoning

Heeft u de presentatie door Jaap van Dissel (de topman van het RIVM) op 18 mrt 2020 ook gevolgd. (https://www.youtube.com/watch?v=DprK2f_Yb8w) Dan zal u misschien niet ontgaan zijn dat de presentatie inhoudelijk een jammerlijke vertoning was. Van enig wetenschappelijk niveau was geen sprake. De presentatie werd gevolgd door een vragenronde. Maar in plaats dat de vragensteller tegemoet werd gekomen om de vragen scherper en nuttiger te maken en zo nodig te herformuleren, werd er regelmatig om de hete brei heen gedraaid en vragen min of meer gepareerd. En dat mogen politici dan misschien af en toe wel doen maar dat hoort niet thuis bij een instituut dat min of meer los van politiek geweld zijn wetenschappelijke werk moet doen. Door de Kamerleden werden overigens een heel aantal zeer relevante vragen gesteld, waar naar mijn menig onvoldoende antwoord op kwam.

Het is de taak van onze politici om over deze materie een zo goed mogelijk besluit te nemen, en ja, zelfs over leven of dood, maar met deze info zijn de consequenties van de opties niet duidelijk.

Ik licht er één aspect uit: De grafieken over aantallen besmette mensen en de benodigde IC-capaciteit. Je had natuurlijk gehoopt dat dat simulaties zouden zijn, waarbij er inzicht in de aannames werd verstrekt. Maar helaas het was slechts een in principe stilering van hetgeen zou kunnen gebeuren, zonder ook maar enige kwantitatieve maat. En niet alleen dat. De indruk die met deze plaatjes wordt gewekt is dat de curve van besmette mensen, door heel geleidelijke beïnvloeding zo kan worden gemanipuleerd dat je onder de benodigde IC- capaciteit blijft van zeg 2000 bedden op het maximum van de intensiteit van de klok-vormige curve van besmette mensen.

Dat zal op die manier nooit haalbaar zijn.

Ik zal proberen een handreiking te doen aan diegenen die proberen te begrijpen hoe de ontwikkeling van het virus zich in Nederland mogelijk kan ontwikkelen en met daaraan gekoppeld de benodigde IC- capaciteit en aantal te verwachten doden en de aannames die daarbij horen. En niet te vergeten de dingen die we nog niet weten of onvoldoende.

Alle varianten waarover gesproken wordt, zijn niet echt anders. Dat maakt de zaak iets overzichtelijker.We hebben maar één knopje waar we aan kunnen draaien en dat is de snelheid waarmee het virus zich kan verspreiden.

In het meest eenvoudige model wordt de snelheid van verspreiding door 2 componenten beïnvloed. Het percentage (s) van mensen wat nog besmet kan worden en een factor (f) waarmee de intrinsieke snelheid van het virus kan worden afgeremd. De R_effectief wordt dan R_eff = R0/f.

De factor f wordt bepaald door de maatregelen die je neemt (social distancing). En de fractie s wordt beïnvloed door opgebouwd immuniteit doordat je ziek bent geworden en weer genezen bent en mogelijk door natuurlijke immuniteit.

Voorts neem ik aan dat het werkelijke aantal besmettingen een factor 5 hoger ligt dan het RIVM registreert. Dat maakt voor de modellering niet zoveel uit behalve dan dat je 5 keer zo snel groepsimmuniteit zou kunnen opbouwen. Maar ik zal laten zien dat we daar nog ongelooflijk ver vandaan zullen blijven.

We beginnen met het geval dat we niets doen. Dan raast de epidemie in een paar maanden tijd over ons heen met op het maximum 1,1 miljoen zieken en 65.000 benodigde IC-bedden indien de verblijfsduur op de IC 20 dagen is.

Dat gebeurt er als je echt niets doet. De realiteit zal anders worden want zodra er duizenden slachtoffers gaan vallen gaat het publiek zelf maatregelen nemen door massaal thuis te blijven. Dan gaat men uit zichzelf ook niet meer joggen in het park, met hele horden op het strand wandelen, enz.  

En dan krijgen we vanzelf een andere situatie. Het probleem is dan wel dat we veel te laat zijn om het aantal patiënten met de beschikbare IC capaciteit ook maar enigszins te matchen.

Hier moeten we echt niet aan denken, dan wordt het erger dan in Italië. Zie ook fig 1 en fig 1b.

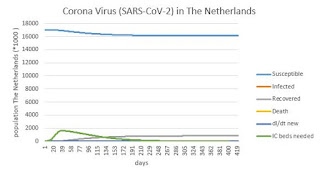
Fig 1a Ontwikkeling in de tijd van aantal besmette mensen, indien we geen maatregelen nemen. Het aantal benodigde IC bedden moet niet met 1000 vermenigvuldig worden. Een schrikbarend aantal van 65.000 IC bedden benodigd, indien we uitgaan van een verblijfsduur van 20 dagen op de IC.

Fig 1b Ontwikkeling in de tijd van aantal besmette mensen, indien we geen maatregelen nemen. R_eff % R0 is het de effectieve R in procenten van R0 door de maatregel. Hier dus constant 100%. Het aantal doden wordt dan 50.000, maar dat kan een factor 2 afwijken met iets andere parameters. Op het maximum 1,1 miljoen besmette mensen. Na afloop 10 miljoen die de ziekte hebben gehad en voor groepsimmuniteit kunnen zorgen.

Dan gaan we naar het geval van een echte lockdown, waarbij men dus niet meer zijn huis uitkomt, en zelfs de voedselvoorziening tot een halt komt. Dan komen we dus om van de honger. Maar het virus is na een maandje ook weg. En ik trek het alleen maar even in het belachelijke door, om aan te geven dat de reële opties op een glijdende schaal tussen de genoemde 2 uiterste opties in liggen. Het gaat om een beetje meer of een beetje minder maatregelen. Daar moeten we ergens een balans in zien te vinden.

Nu de huidige situatie, waarin er een aantal social distancing maatregelen zijn genomen die vandaag 23 maart nog iets zijn aangescherpt omdat zo’n 10 % van de bevolking de regels nog niet erg nauwgezet naleeft. Kortom horeca dicht, scholen dicht, veel niet-essentiële winkel sluiten uit zichzelf al, geen samenscholingen van meer de 3 mensen en een sociale afstand 1,5 meter. En we gaan zien hoe dat gaat uitpakken.

Stel nu eens dat de factor f zodanig kan worden beïnvloed door de maatregelen dat R_eff tot 58 % van R0 kan worden gereduceerd. Dan is dus de verspreidingssnelheid fors lager. Het resultaat daarvan ziet u in fig 2a en fig 2b. Zodra het virus aanzienlijk is teruggedrongen relaxen we de maatregelen en laten R_eff oplopen tot net onder de een, waardoor het virus geen kans meer krijgt.

Dat vereist een heel goed monitoring instrument, want zodra het virus de kop weer opsteekt moet je mogelijk zwaarder ingrijpen. Dus zoals de WHO aanbeveelt: testen, testen, testen.

Hiermee hebben we dus tijd gekocht om medicijnen te ontwikkelen, een vaccin te ontwikkelen en om meer research  te doen om betere maatregelen te kunnen nemen. Er zijn nog heel veel vragen te beantwoorden. Hoe effectief is het gebruik van mondkapjes eigenlijk? En kunnen we dat ook kwantificeren? En hoe verhoudt zich dat tot andere maatregelen? En hoe ernstig is het besmettings risico via de voedsel keten, in supermarkten op plastic verpakkingen, enz. En zo zijn er nog tientallen dingen te verzinnen, waar we nu onvoldoende antwoord op hebben.

Fig 2a Ontwikkeling in de tijd van aantal besmette mensen, indien we voldoende maatregelen nemen in de hoop om onder de beschikbare IC bedden capaciteit te blijven. Het aantal benodigde IC bedden moet niet met 1000 vermenigvuldig worden. Het IC bedden benodigd indien we uitgaan van een verblijfsduur van 20 dagen op de IC ligt in dit geval onder de 2000 bedden.

Fig 2b Ontwikkeling in de tijd van aantal besmette mensen, indien we stevige maatregelen nemen. R_eff % R0 is de effectieve R in procenten van R0 door de maatregel. Hier wordt R_eff verlaagt tot 58 % van R0 en nadat het virus aanzienlijk gereduceerd is worden de maatregelen iets relaxed zodanig dat de R_eff net onder de 1 blijft waardoor het virus in principe geen kans meer krijgt. Het aantal doden wordt dan 1750, maar dat kan een factor 2 afwijken met iets andere parameters. Op het maximum zijn er 30.000 besmette mensen. Na afloop zijn er 350.000 mensen die de ziekte hebben gehad en die nog niet bij benadering voor groepsimmuniteit kunnen zorgen.

Wat tevens opvalt is dat als je voor deze strategie kiest dat je er als de wie de weerga bij moet zijn om met de maatregelen van start te gaan. Hoe is het mogelijk dat er pas in maart maatregelen zijn genomen. In december was al duidelijk dat er in China iets aan de hand was. Sterker nog, we weten al honderden jaren dat een virus of bacterie op elk moment kan toeslaan.  Dus dat betekent dat de draaiboeken al lang en breed klaar kunnen liggen. We weten nog niet wat er gebeurt, maar wel dat je snel moet handelen als je op deze strategie mikt.

Laten we ook eens kijken naar een alternatief om de curve van besmette mensen zo te sturen dat op het maximum net de maximum IC bedden capaciteit wordt opgesoupeerd.

We laten dan het virus min of meer gecontroleerd zijn gang met een R_eff constant net boven de een. Dat is de situatie waar we nu bijna in zitten. Dat is dus met iets minder maatregelen dan in variant 2. Het resultaat zien we in fig 3a en fig 3b.

Fig 3a Ontwikkeling in de tijd van aantal besmette mensen, indien we voldoende maatregelen nemen in de hoop om onder de beschikbare IC bedden capaciteit te blijven. Het aantal benodigde IC bedden moet niet met 1000 vermenigvuldig worden. Het IC bedden benodigd indien we uitgaan van een verblijfsduur van 20 dagen op de IC ligt in dit geval onder de 2000 bedden. Het aantal genezen mensen is opgelopen tot 5 %, nog steeds geen reden om de maatregelen helemaal te schrappen, we zitten immers nog ver van groepsimmuniteit verwijderd.

 

Fig 3b Ontwikkeling in de tijd van aantal besmette mensen, indien we nu maatregelen nemen om net onder de IC-capaciteit uit te komen. R_eff % R0 is het de effectieve R in procenten van R0 door de maatregel. Hier wordt R_eff verlaagt tot 67 % van R0 en nadat het virus aanzienlijk gereduceerd is worden de maatregelen iets relaxed zodanig dat de R_eff net onder de 1 blijft waardoor het virus in principe geen kans meer krijgt. Het aantal doden wordt dan 4200, maar dat kan een factor 2 afwijken met iets andere parameters. Op het maximum zijn er 20.000 besmette mensen. Na afloop zin er 850.000 mensen die de ziekte hebben gehad en nog niet bij benadering voor groepsimmuniteit kunnen zorgen zonder maatregelen.

Nu het bedroevende geval dat we de maatregel zodanig relaxed instellen dat we de IC-capaciteit zolang ten volle gaan benutten tot we groepsimmuniteit hebben opgebouwd. Een ethisch dilemma want hier gaan veel doden vallen.

We verlagen de R_eff weer op dezelfde manier als in het voorgaande voorbeeld, maar laten R_eff relaxen, gaandeweg als de factor s zijn bijdrage levert. Hierdoor blijft de momentane snelheid van het virus constant. Er worden evenveel mensen ziek als dat er beter worden of doodgaan. Het resultaat ziet u in fig 4a en fig 4b.

Fig 4a Ontwikkeling in de tijd van aantal besmette mensen, indien we voldoende maatregelen nemen in de hoop om gedurende de gehele tijd net onder de beschikbare IC-bedden capaciteit te blijven totdat groepsimmuniteit is verkregen. Het aantal benodigde IC-bedden moet niet met 1000 vermenigvuldig worden. Het IC-bedden benodigd indien we uitgaan van een verblijfsduur van 20 dagen op de IC ligt in dit geval ongeveer 2000 bedden. Het aantal genezen mensen zal na ruim 1,5 jaar opgelopen tot 66 %. Er is groepsimmuniteit en alle maatregelen kunnen worden opgeheven. Het aantal te betreuren doden ongeveer 50.000.

Fig 4b Ontwikkeling in de tijd van aantal besmette mensen, indien we voldoende maatregelen nemen in de hoop om gedurende de gehele tijd net onder de beschikbare IC-bedden capaciteit te blijven totdat groepsimmuniteit is verkregen. R_eff % R0 is de effectieve R in procenten van R0 door de maatregel. Hier wordt R_eff verlaagt tot 67 % van R0 en nadat het virus aanzienlijk gereduceerd is worden de maatregelen geleidelijk aan worden relaxed zodanig dat de maximum IC-capaciteit constant wordt benut. Het aantal doden wordt na ruim 1,5 jaar 50.000, maar dat kan een factor 2 afwijken met iets andere parameters. Op het maximum zijn er 20.000 besmette mensen. Na afloop zijn er 10 miljoen mensen die de ziekte hebben gehad, die voor groepsimmuniteit zorgen.

Tot slot nog de laatste variant, die overigens in het Nederlandse stadium niet meer mogelijk is. Hierbij proberen we de curve van besmette mensen, als die maximaal is, met een pakket van maatregelen, zodanig te manipuleren dat op dat punt de maximum IC-capaciteit wordt verbruikt.

Hiervoor zijn we echter te laat. Om het toch te laten zien vervroeg ik de maatregel tot dag 1. R_eff reduceren we tot net boven de 1. Zie fig 5a en fig 5b.

Uiteindelijk zullen er 8000 doden vallen en tegen de 2 miljoen mensen weer beter worden, waarmee helaas weer geen groepsimmuniteit is opgebouwd.

Ik wijs er nogmaals op dat dit in Nederland nu geen optie meer is, omdat we al te ver gevorderd zijn in de tijd en het virus al om zich heen heeft gegrepen en we al nagenoeg aan de maximum IC-capaciteit zitten.

Fig 5a Ontwikkeling in de tijd van aantal besmette mensen, indien we vanaf dag 1 voldoende maatregelen nemen in de hoop om gedurende de gehele tijd net onder de beschikbare IC-bedden capaciteit te blijven. Het aantal benodigde IC-bedden moet niet met 1000 vermenigvuldig worden. Het IC-bedden benodigd indien we uitgaan van een verblijfsduur van 20 dagen op de IC ligt in dit geval op ongeveer 2000 bedden. Het aantal genezen mensen zal na ruim 1 jaar zijn opgelopen tot 12 %. Er is nog geen groepsimmuniteit en de maatregelen moet gehandhaafd worden, zij het iets verminderd. Het aantal te betreuren doden ongeveer 8.000.

Fig 5b Ontwikkeling in de tijd van aantal besmette mensen, indien we vanaf dag 1 voldoende maatregelen nemen in de hoop om gedurende de gehele tijd net onder de beschikbare IC-bedden capaciteit te blijven. R_eff % R0 is de effectieve R in procenten van R0 door de maatregel. Hier wordt R_eff verlaagt tot net boven de 1, waarbij op het maximum de IC-capaciteit geheel wordt benut. Het aantal doden wordt na ruim 1 jaar 8.000, maar dat kan een factor 2 afwijken met iets andere parameters. Op het maximum zijn er 20.000 besmette mensen. Na afloop zijn er bijna 2 miljoen mensen die de ziekte hebben gehad, die helaas nog niet voor groepsimmuniteit zorgen. De maatregelen moeten gehandhaafd blijven, zij het in iets mildere vorm.

Het valt overigens te betwijfelen of je met een incubatie tijd van 1 à 2 weken de aantallen zieken heel fijnzinnig zou kunnen regelen. Misschien moet ik het iets sterker zeggen. Vergeet dat maar. 

Enig licht punt puntje is dat we 24 mrt 2020 al 2 dagen hebben gehad met weliswaar forse hoeveelheid doden, maar het aantal nieuwe besmettingen is in procentuele zin afgenomen van 25 % tot 12 %. Dat is het eerste begin van een kentering die dan nog wel moet doorzetten.

Het tweede punt waar je vraagtekens bij kunt bijzetten is de bewering op de website van het RIVM dat het voldoende is om 1 dag klachtenvrij te zijn om niet meer besmettelijk te zijn met als enige argumentatie dat je ergens een streep moet trekken. Het advies van de WHO met 1 à 2 weken vormt hiermee een schril contrast. Juist als je nog niet voldoende immuniteit opbouwt om groepsimmuniteit te hebben kun je je afvragen of je dan niet beter voor de veilige variant van het WHO moet kiezen, maar ik laat me door research graag anders overtuigen.

En ja, de bovenstaande simulaties kunnen met betere modellen wat beter en de parameters moeten beter bepaald worden, en je moet leeftijdsklassen gebruiken en de verschillen in maatregelen tussen groepen meenemen, enz. Neemt niet weg dat de conclusie overeind blijft.

Al met al lijkt optie 2 in fig 2a en fig 2b nog de meest ethische en effectieve methode. Merk op dat dat eigenlijk overeenkomt met de ‘lockdown’ die door het RIVM getoond werd. In Nederland hebben we nu geen andere mogelijkheid meer. Het goede nieuws is dat daar door het kabinet op wordt ingezet. En gelukkig sinds 23 maart 2020 met een tandje erbij. Het is vandaag nog te vroeg om te zeggen dat we het gaan redden of dat er nog een paar tanden bij moeten worden gezet.

Er is ook als mogelijkheid genoemd om die groepen ziek te laten worden die er minder last van hebben of waar de overlijdenskans kleiner is, met name de jongeren in dit geval. Onder maatschappelijk druk zijn de scholen uiteindelijk toch gesloten. En zelfs als je dat zou doen dan is nog de vraag of dat voor de ouderen voldoende groepsimmuniteit oplevert. 

Het slechte nieuws is dat de maatregelen te laat zijn genomen. In de politiestaat Singapore zijn binnen 1 week maatregelen afgekondigd en dat gaat daar iets rigoureuzer dan bij ons. Nu pleit ik niet voor een politiestaat, maar een dergelijke crisis vereist nu eenmaal een andere aanpak dan een poldermodel. Hier moet een crisismanager worden ingezet die maatregelen kan treffen, dat kan zelfs de minister-president zijn, die tijdelijk meer overrulende bevoegdheden krijgt als het kabinet er niet snel genoeg uit dreigt te komen.

We moeten het hebben van snelheid van handelen op grond van nu beschikbare betrouwbare informatie, want research en dingen uitzoeken doen we gaandeweg wel. Nu moeten we beslissingen nemen.

Maar dit alles moeten ze bij het RIVM toch ook weten. Wat is er aan de hand?